Total Lunar Eclipse of -1180 Nov 25 (1181 Nov 25 BCE)

Fred Espenak

Introduction

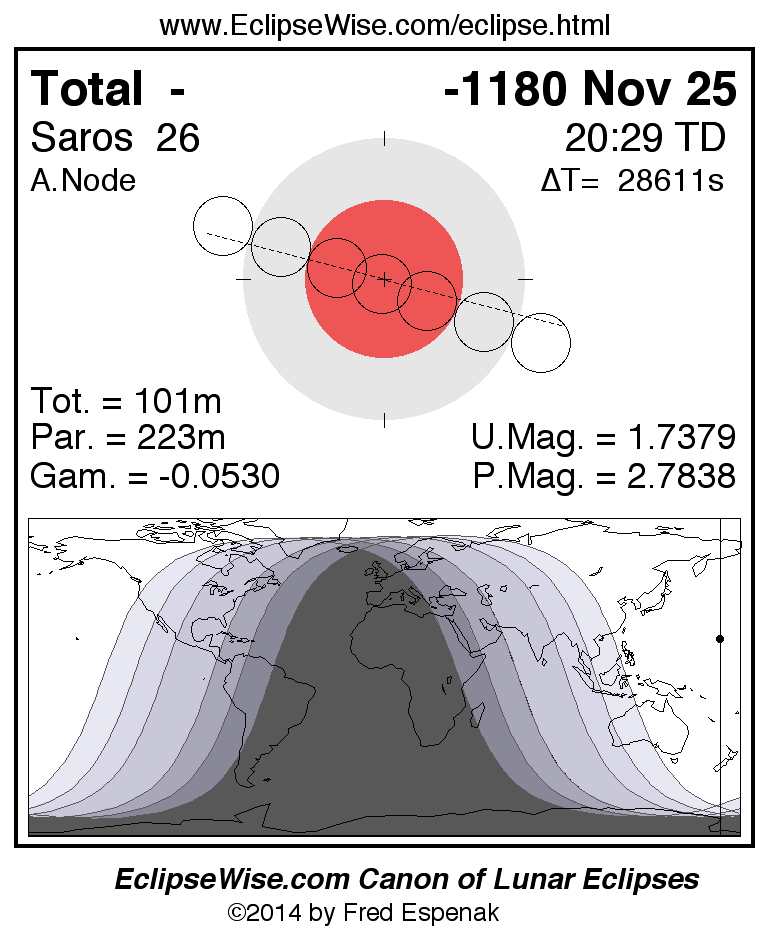
The Total Lunar Eclipse of -1180 Nov 25 (1181 Nov 25 BCE) is visible from the geographic regions shown on the map to the right. The diagram above the map depicts the Moon's path with respect to Earth's umbral and penumbral shadows. Click on the figure to enlarge it. For an explanation of the features appearing in the figure, see Key to Lunar Eclipse Figures.

The instant of greatest eclipse takes place on -1180 Nov 25 at 20:28:40 TD (12:31:53 UT1). This is 6.9 days before the Moon reaches apogee. During the eclipse, the Moon is in the constellation Gemini. The synodic month in which the eclipse takes place has a Brown Lunation Number of -38368.

The eclipse belongs to Saros 26 and is number 43 of 87 eclipses in the series. All eclipses in this series occur at the Moon’s ascending node. The Moon moves southward with respect to the node with each succeeding eclipse in the series and gamma decreases.

This total eclipse is central meaning the Moon’s disk actually passes through the axis of Earth’s umbral shadow. It has an umbral eclipse magnitude of 1.7379, and Gamma has a value of -0.0530. Because they are so deep, such eclipses typically have the longest total phases. In this case, the duration of totality lasts 101.2 minutes. That qualifies the eclipse as a member of a select class of exceptionally long total eclipses with durations exceeding 100 minutes.

The total lunar eclipse of -1180 Nov 25 is preceded two weeks earlier by a partial solar eclipse on -1180 Nov 11, and it is followed two weeks later by a partial solar eclipse on -1180 Dec 11.

These eclipses all take place during a single eclipse season.

The eclipse predictions are given in both Terrestrial Dynamical Time (TD) and Universal Time (UT1). The parameter ΔT is used to convert between these two times (i.e., UT1 = TD - ΔT). ΔT has a value of 28607.0 seconds for this eclipse. The uncertainty in ΔT is 1013.4 seconds corresponding to a standard error in longitude of the eclipse visibility zones of 4.23°.

The following links provide maps and data for the eclipse.

The tables below contain detailed predictions and additional information on the Total Lunar Eclipse of -1180 Nov 25 .

Eclipse Data: Total Lunar Eclipse of -1180 Nov 25

Eclipse Characteristics
Parameter Value
Penumbral Magnitude 2.78377
Umbral Magnitude 1.73792
Gamma-0.05304
Epsilon 0.0505°
Opposition Times
Event Calendar Date & Time Julian Date
Greatest Eclipse -1180 Nov 25 at 20:28:39.6 TD (12:31:52.6 UT1) 1290392.022136
Ecliptic Opposition -1180 Nov 25 at 20:28:03.9 TD (12:31:16.9 UT1) 1290392.021723
Equatorial Opposition -1180 Nov 25 at 20:26:27.8 TD (12:29:40.8 UT1) 1290392.020611
Geocentric Coordinates of Sun and Moon
-1180 Nov 25 at 20:28:39.6 TD (12:31:52.6 UT1)
Coordinate Sun Moon
Right Ascension15h25m44.0s03h25m48.4s
Declination-19°03'27.0"+19°00'36.3"
Semi-Diameter 16'17.1" 15'34.2"
Eq. Hor. Parallax 09.0" 0°57'08.7"
Geocentric Libration of Moon
Angle Value
l 5.4°
b 0.0°
c -12.9°
Earth's Shadows
Parameter Value
Penumbral Radius 1.2358°
Umbral Radius 0.6930°
Prediction Paramaters
Paramater Value
Ephemerides JPL DE406
ΔT 28607.0 s
Shadow Rule Danjon
Shadow Enlargement 1.010
Saros Series 26 (43/87)

Explanation of Lunar Eclipse Data Tables

Eclipse Contacts: Total Lunar Eclipse of -1180 Nov 25

Lunar Eclipse Contacts
Eclipse Event Contact Time
TD		 Time
UT1		 Zenith Latitude Zenith Longitude Position Angle Axis Distance
Penumbral BeginsP117:33:08.509:36:21.518°27.2'N147°36.2'W 247.7° 1.4969°
Partial BeginsU118:36:54.210:40:07.218°39.4'N163°00.3'W 246.6° 0.9535°
Total BeginsU219:38:04.411:41:17.418°51.1'N177°46.7'W 243.0° 0.4338°
Greatest EclipseGreatest20:28:39.612:31:52.619°00.6'N170°00.2'E 159.7° 0.0505°
Total EndsU321:19:13.513:22:26.519°10.1'N157°47.5'E 76.4° 0.4333°
Partial EndsU422:20:22.814:23:35.819°21.4'N143°01.4'E 72.8° 0.9516°
Penumbral EndsP423:24:17.515:27:30.519°33.2'N127°35.4'E 71.7° 1.4938°
Eclipse Durations
Eclipse Phase Duration
Penumbral (P4 - P1)05h51m09.0s
Partial (U4 - U1)03h43m28.6s
Total (U3 - U2)01h41m09.2s

Explanation of Lunar Eclipse Contacts Table

Polynomial Besselian Elements: Total Lunar Eclipse of -1180 Nov 25

Polynomial Besselian Elements
-1180 Nov 25 at 20:00:00.0 TD (=t0)
n x y d f1 f2 f3
0 -0.21130 -0.13211 -0.3325 1.23604 0.69321 0.25956
1 0.47917 0.17751 -0.0002 -0.00041 -0.00040 -0.00011
2 -0.00017 -0.00019 0.0000 -0.00000 -0.00000 -0.00000
3 -0.00001 -0.00000 - - - -

At time t1 (decimal hours), each besselian element is evaluated by:

x = x0 + x1*t + x2*t2 + x3*t3 (or x = Σ [xn*tn]; n = 0 to 3)

where: t = t1 - t0 (decimal hours) and t0 = 20.000

Explanation of Besselian Elements

Links for the Total Lunar Eclipse of -1180 Nov 25 (1181 Nov 25 BCE)

Links to Additional Lunar Eclipse Information

Calendar

The Gregorian calendar (also called the Western calendar) is internationally the most widely used civil calendar. It is named for Pope Gregory XIII, who introduced it in 1582. On this website, the Gregorian calendar is used for all calendar dates from 1582 Oct 15 onwards. Before that date, the Julian calendar is used. For more information on this topic, see Calendar Dates.

The Julian calendar does not include the year 0. Thus the year 1 BCE is followed by the year 1 CE (See: BCE/CE Dating Conventions). This is awkward for arithmetic calculations. Years in this catalog are numbered astronomically and include the year 0. Historians should note there is a difference of one year between astronomical dates and BCE dates. Thus, the astronomical year 0 corresponds to 1 BCE, and astronomical year -1 corresponds to 2 BCE, etc..

Eclipse Predictions

Predictions for the Total Lunar Eclipse of -1180 Nov 25 were generated using the JPL DE406 solar and lunar ephemerides. The lunar coordinates were calculated with respect to the Moon's Center of Mass. The predictions are given in both Terrestrial Dynamical Time (TD) and Universal Time (UT1). The parameter ΔT is used to convert between these two times (i.e., UT1 = TD - ΔT). ΔT has a value of 28607.0 seconds for this eclipse. The uncertainty in ΔT is 1013.4 seconds corresponding to a standard error in longitude of the eclipse visibility zones of 4.23°.

Acknowledgments

Some of the content on this web site is based on the book Thousand Year Canon of Lunar Eclipses 1501 to 2500. All eclipse calculations are by Fred Espenak, and he assumes full responsibility for their accuracy.

Permission is granted to reproduce this data when accompanied by an acknowledgment:

"Eclipse Predictions by Fred Espenak, www.EclipseWise.com"

The use of diagrams and maps is permitted provided that they are NOT altered (except for re-sizing) and the embedded credit line is NOT removed or covered.