Solar Eclipse Prime Page

Annular Solar Eclipse of -1332 Feb 19 (1333 Feb 19 BCE)

Fred Espenak

Introduction

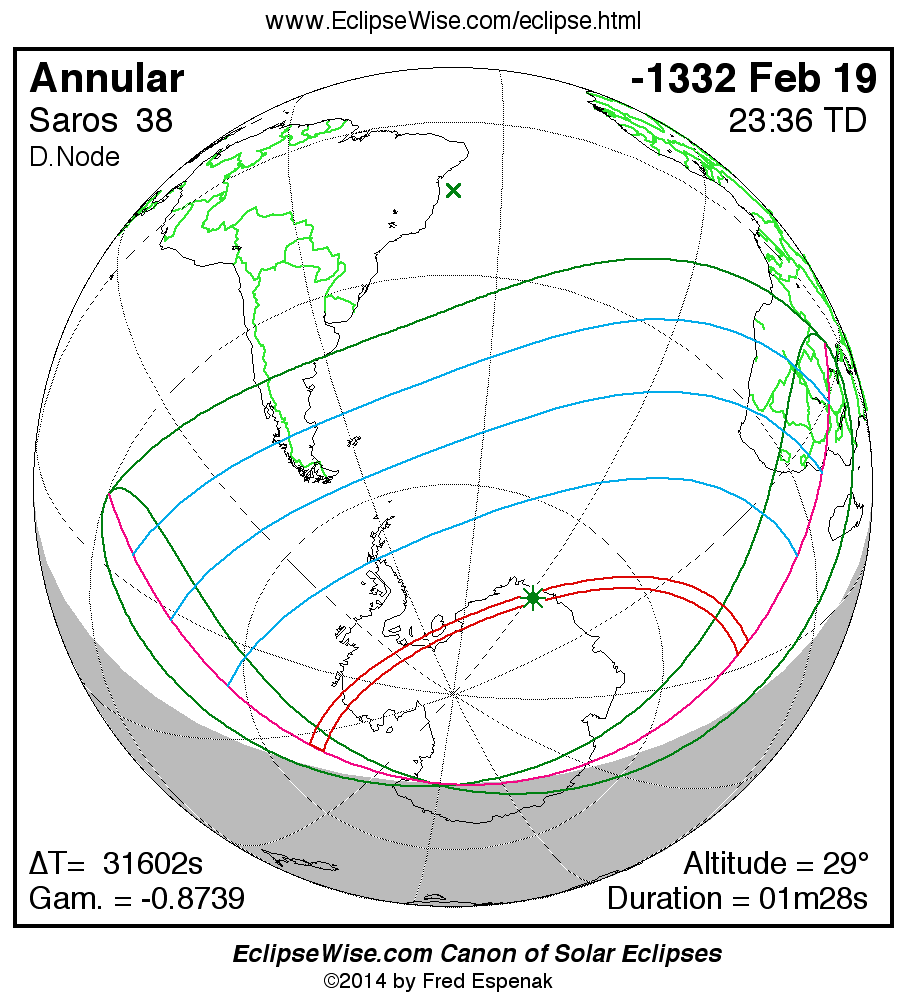
eclipse map

The Annular Solar Eclipse of -1332 Feb 19 (1333 Feb 19 BCE) is visible from the geographic regions shown on the map to the right. Click on the map to enlarge it. For an explanation of the features appearing in the map, see Key to Solar Eclipse Maps.

The instant of greatest eclipse takes place on -1332 Feb 19 at 23:35:36 TD (14:48:58 UT1). This is 6.8 days before the Moon reaches apogee. During the eclipse, the Sun is in the constellation Pisces. The synodic month in which the eclipse takes place has a Brown Lunation Number of -40257.

The eclipse belongs to Saros 38 and is number 23 of 73 eclipses in the series. All eclipses in this series occur at the Moon’s descending node. The Moon moves northward with respect to the node with each succeeding eclipse in the series and gamma increases.

The annular solar eclipse of -1332 Feb 19 is preceded two weeks earlier by a total lunar eclipse on -1332 Feb 06.

These eclipses all take place during a single eclipse season.

The eclipse predictions are given in both Terrestrial Dynamical Time (TD) and Universal Time (UT1). The parameter ΔT is used to convert between these two times (i.e., UT1 = TD - ΔT). ΔT has a value of 31598.4 seconds for this eclipse. The uncertainty in ΔT is 1406.6 seconds corresponding to a standard error in longitude of the eclipse path of ± 5.88°.

The following links provide maps and data for the eclipse.

The tables below contain detailed predictions and additional information on the Annular Solar Eclipse of -1332 Feb 19 .

Eclipse Data: Annular Solar Eclipse of -1332 Feb 19

Eclipse Characteristics
Parameter Value
Eclipse Magnitude 0.97894
Eclipse Obscuration 0.95832
Gamma-0.87389
Conjunction Times
Event Calendar Date and Time Julian Date
Greatest Eclipse -1332 Feb 19 at 23:35:36.0 TD (14:48:57.6 UT1) 1234594.117334
Ecliptic Conjunction -1332 Feb 19 at 23:45:17.1 TD (14:58:38.7 UT1) 1234594.124060
Equatorial Conjunction -1332 Feb 19 at 23:13:35.3 TD (14:26:56.9 UT1) 1234594.102048
Geocentric Coordinates of Sun and Moon
-1332 Feb 19 at 23:35:36.0 TD (14:48:57.6 UT1)
Coordinate Sun Moon
Right Ascension21h25m09.8s21h25m55.4s
Declination-15°27'16.6"-16°15'44.8"
Semi-Diameter 15'59.1" 15'32.1"
Eq. Hor. Parallax 08.8" 0°57'00.7"
Geocentric Libration of Moon
Angle Value
l 5.2°
b 1.2°
c -20.1°
Prediction Paramaters
Paramater Value
Ephemerides JPL DE406
ΔT 31598.4 s
k (penumbra) 0.2725076
k (umbra) 0.2722810
Saros Series 38 (23/73)

Explanation of Solar Eclipse Data Tables

Penumbral Shadow Contacts and Extremes: Annular Solar Eclipse of -1332 Feb 19

Contacts of Penumbral Shadow with Earth
Contact Event Contact Time
TD		 Time
UT1		 Latitude Longitude
First External ContactP121:12:25.712:25:47.344°56.0'S107°39.1'W
Last External ContactP401:59:02.217:12:23.820°45.9'S022°44.0'E
Extreme Northern and Southern Path Limits of Penumbra
Contact Event Contact Time
TD		 Time
UT1		 Latitude Longitude
North Extreme Path Limit 1N121:42:45.712:56:07.430°29.3'S108°34.5'W
South Extreme Path Limit 1S101:28:36.116:41:57.705°55.9'S025°59.1'E

Explanation of Penumbral Shadow Contacts and Extremes Tables

Umbral Shadow Contacts and Extremes: Annular Solar Eclipse of -1332 Feb 19

Contacts of Umbral Shadow with Earth
Contact Event Contact Time
TD		 Time
UT1		 Latitude Longitude
First External ContactU122:40:10.913:53:32.567°19.2'S155°00.2'W
First Internal ContactU222:43:54.013:57:15.668°29.9'S159°05.0'W
Last Internal ContactU300:27:31.215:40:52.847°03.1'S056°52.5'E
Last External ContactU400:31:19.815:44:41.445°28.2'S054°57.9'E
Extreme Northern and Southern Path Limits of Umbra
Contact Event Contact Time
TD		 Time
UT1		 Latitude Longitude
North Extreme Path Limit 1N122:40:22.013:53:43.767°14.0'S154°50.2'W
South Extreme Path Limit 1S122:43:43.513:57:05.168°34.5'S159°15.9'W
North Extreme Path Limit 2N200:31:08.415:44:30.045°21.3'S054°56.8'E
South Extreme Path Limit 2S200:27:42.015:41:03.647°09.6'S056°53.8'E

Explanation of Umbral Shadow Contacts and Extremes Tables

Central Line Extremes and Duration: Annular Solar Eclipse of -1332 Feb 19

Extreme Limits of the Central Line
Contact Event Contact Time
TD		 Time
UT1		 Latitude Longitude
Extreme Central Line Limit 1C122:42:00.913:55:22.567°54.2'S156°57.8'W
Extreme Central Line Limit 2C200:29:27.015:42:48.646°14.7'S055°53.8'E

Explanation of Central Line Extremes Table

Greatest Eclipse and Greatest Duration
Event Time
TD		 Time
UT1		 Latitude Longitude Sun
Altitude		 Sun
Azimuth		 Path Width Central
Duration
Greatest Eclipse23:35:36.014:48:57.672°21.3'S130°09.0'W 28.7° 315.9° 155.4 km01m27.86s
Greatest Duration22:42:00.913:55:22.567°54.2'S203°02.2'E 0.0° 135.1° 237.2 km01m35.99s

Explanation of Greatest Eclipse and Greatest Duration

Polynomial Besselian Elements: Annular Solar Eclipse of -1332 Feb 19

Polynomial Besselian Elements
-1332 Feb 20 at 00:00:00.0 TD (=t0)
n x y d l1 l2 μ
0 0.40584 -0.80423 -15.4474 0.55435 0.00815 175.5280
1 0.52462 0.11858 0.0127 0.00011 0.00011 15.0020
2 -0.00006 0.00013 0.0000 -0.00001 -0.00001 0.0000
3 -0.00001 -0.00000 - - - -
Tan ƒ1 0.0046736
Tan ƒ2 0.0046504

At time t1 (decimal hours), each besselian element is evaluated by:

x = x0 + x1*t + x2*t2 + x3*t3 (or x = Σ [xn*tn]; n = 0 to 3)

where: t = t1 - t0 (decimal hours) and t0 = 0.000

Explanation of Polynomial Besselian Elements

Links for the Annular Solar Eclipse of -1332 Feb 19 (1333 Feb 19 BCE)

Links to Additional Solar Eclipse Information

Calendar

The Gregorian calendar (also called the Western calendar) is internationally the most widely used civil calendar. It is named for Pope Gregory XIII, who introduced it in 1582. On this website, the Gregorian calendar is used for all calendar dates from 1582 Oct 15 onwards. Before that date, the Julian calendar is used. For more information on this topic, see Calendar Dates.

The Julian calendar does not include the year 0. Thus the year 1 BCE is followed by the year 1 CE (See: BCE/CE Dating Conventions). This is awkward for arithmetic calculations. Years in this catalog are numbered astronomically and include the year 0. Historians should note there is a difference of one year between astronomical dates and BCE dates. Thus, the astronomical year 0 corresponds to 1 BCE, and astronomical year -1 corresponds to 2 BCE, etc..

Eclipse Predictions

Predictions for the Annular Solar Eclipse of -1332 Feb 19 were generated using the JPL DE406 solar and lunar ephemerides. The lunar coordinates were calculated with respect to the Moon's Center of Mass. The predictions are given in both Terrestrial Dynamical Time (TD) and Universal Time (UT1). The parameter ΔT is used to convert between these two times (i.e., UT1 = TD - ΔT). ΔT has a value of 31598.4 seconds for this eclipse. The uncertainty in ΔT is 1406.6 seconds corresponding to a standard error in longitude of the eclipse path of ± 5.88°.

Acknowledgments

Some of the content on this website is based on the book Thousand Year Canon of Solar Eclipses 1501 to 2500. All eclipse calculations are by Fred Espenak, and he assumes full responsibility for their accuracy.

Permission is granted to reproduce eclipse data when accompanied by a link to this page and an acknowledgment:

"Eclipse Predictions by Fred Espenak, www.EclipseWise.com"

The use of diagrams and maps is permitted provided that they are NOT altered (except for re-sizing) and the embedded credit line is NOT removed or covered.